Elektrodinamika – fizikaning elektr zaryadlarining o’zaro ta’sirini o’rganuvchi bo’limi. U qo’zg’almas zaryadlar o’zaro ta’sirining xususiy va eng sodda holi sifatida elektrostatikani o’z ichiga oladi. Harakatlanuvchi zaryadlar orasidagi o’zaro ta’sirni elektrodinamikada elektr va magnit maydon iboralaridan foydalanish tufayligina tavsiflash mumkin. Shuni ham e’tiborga olish kerakki, ko’pincha, bir maydonni ikkinchisidan ajratish mumkin emas va shuning uchun elektromagnit maydon to’g’risida gapiriladi. Tajriba shuni ko’rsatadiki, harakatlanuvchi zaryadga ta’sir etuvchi kuchni ikki qo’shiluvchining yig’indisi deb tasavvur qilish mumkin:
Birinchi qo’shiluvchi zaryadning harakatlanishiga yoki uning qo’zg’almay turishiga bog’liq emas, shuning uchun elektr kuchi elektrostatikadagi ifodaning aynan o’ziga teng:
bu yerda q – zaryad mikdori, 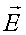 – elektr maydon kuchlanganligi. Lorents kuchi deb ataladigan ikkinchi qo’shiluvchi zaryad tezligiga bog’liq va magnit maydonga bog’langan. Agar elektr maydon kuchlanganligi har bir nuqtada
– elektr maydon kuchlanganligi. Lorents kuchi deb ataladigan ikkinchi qo’shiluvchi zaryad tezligiga bog’liq va magnit maydonga bog’langan. Agar elektr maydon kuchlanganligi har bir nuqtada 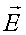 vektor bilan ifodalansa, u holda magnit maydon kattaligi magnit induksiya vektori deyiladigan V vektor bilan ifodalanadi. Elektr maydondan farqli faqat harakatlanuvchi zaryadlar hosil qiladigan magnit maydon vujudga keladi. Lorens kuchiLorens kuchi ifodasi elektr kuchga nisbatan murakkab ko’rinishli bo’lib, absolyut miqdori bo’yicha u:
vektor bilan ifodalansa, u holda magnit maydon kattaligi magnit induksiya vektori deyiladigan V vektor bilan ifodalanadi. Elektr maydondan farqli faqat harakatlanuvchi zaryadlar hosil qiladigan magnit maydon vujudga keladi. Lorens kuchiLorens kuchi ifodasi elektr kuchga nisbatan murakkab ko’rinishli bo’lib, absolyut miqdori bo’yicha u:
ga teng. Lorens kuchi zarraning q zaryadiga, uning 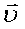 tezligiga proportsional va zaryadning harakat yo’nalishiga bog’liq bo’ladi.
tezligiga proportsional va zaryadning harakat yo’nalishiga bog’liq bo’ladi. 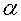 burchak – tezlik vektori va induksiya vektori orasidagi burchak.
burchak – tezlik vektori va induksiya vektori orasidagi burchak.
Lorens kuchining yo’nalishi quyidagicha aniqlanadi: Lorens kuchi har doim magnit induksiya vektoriga perpendikulyar, u esa fazoda ajratib olingan magnit kuchlar ta’sir etmaydigan yo’nalishni ko’rsatadi; bundan tashqari Lorens kuchi vektori zaryad tezligi vektori ga ham perpendikulyardir. Kuchning oxirgi yo’nalishini (masalan, rasmda yuqoriga yoki pastga) chap qo’l qoidasi yordamida aniqlash mumkin (manfiy zaryad uchun kuch yo’nalishi qarama-qarshi tomonga o’zgaradi). Lorens kuchi tezlikka (va zaryadning kuchishiga) perpendikulyar bo’lgani uchun bu kuch bajargan ish har doim nolga teng bo’ladi. Magnit maydon zaryadlangan zarra tezligi kattaligini o’zgartira olmaydi, tezlikning faqat yunalishigina o’zgaradi. Shunday qilib, bir jinsli magnit maydonda (V=const) magnit maydonga perpendikulyar harakatlanayotgan zaryadlangan zarra traektoriyasi aylanadan iborat bo’ladi. Amalda biz, odatda, alohida zaryadlar bilan emas, balki juda ko’p sonli zarralar oqimi bilan ish ko’ramiz. Zaryadlangan zarralar oqimi elektr tok deyiladi, bunda elektr tokning yo’nalishi musbat zaryadlarning harakat yo’nalishiga mos keladi, deb hisoblash qabul qilingan. Vaqt birligida S sirtdan o’tayotgan to’la zaryadga teng miqdor shu sirtdan o’tayotgan tok kuchi deyiladi. Masalan, o’tkazgichdagi tok kuchi 1 s ichida o’tkazgichning butun ko’ndalang kesimidan o’tgan zaryad miqdoriga teng.
O’tkazgichlarda (masalan, metallarda) odatda zaryadlar miqdori juda ko’p bo’ladi va shuning uchun bu zaryadlar juda yaxshi kompensatsiyalangan: musbat va manfiy zaryadlar miqdorlari bir-biriga teng. Demak, o’tkazgichga ta’sir etuvchi elektr kuchlar yig’indisi nolga teng.
O’tkazgichdagi alohida zaryadlarga ta’sir etuvchi magnit kuchlari esa kompensatsiyalanmaydi, chunki o’tkazgichdan tok o’tayotganda undagi musbat va manfiy zaryadlarning harakat tezliklari turlicha bo’ladi. Tokli o’tkazgichga magnit maydonda ta’sir etayotgan kuch 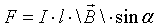 ga teng, bu yerda I – tok kuchi, l – o’tkazgich uzunligi,
ga teng, bu yerda I – tok kuchi, l – o’tkazgich uzunligi, 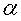 – magnit maydoni va tok yo’nalishi orasidagi burchak. Amper qonuni deyiladigan bu tenglik tarixan Lorens kuchidan oldinroq olingan, shunday bo’lsa ham Amper kuchi – bu o’tkazgichdagi alohida zaryadlarga ta’sir etuvchi Lorens kuchlari yig’indisidan boshqa narsa emas.
– magnit maydoni va tok yo’nalishi orasidagi burchak. Amper qonuni deyiladigan bu tenglik tarixan Lorens kuchidan oldinroq olingan, shunday bo’lsa ham Amper kuchi – bu o’tkazgichdagi alohida zaryadlarga ta’sir etuvchi Lorens kuchlari yig’indisidan boshqa narsa emas.
Shunday qilib, agar bizga elektr va magnit maydon (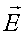 va
va 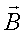 ) ma’lum bo’lsa, u holda hammaga ma’lum qoida bo’yicha harakatlanuvchi zaryadga ta’sir etuvchi kuchlarni (yoki elektr tokni) hisoblash mumkin va shuning uchun harakatlanuvchi zaryadlarning o’zaro ta’sirini hisoblash masalasi elektromagnit maydonni hisoblashga keltiriladi. Elektrodinamikada elektromagnit maydon J. Maksvellning to’rtta tenglamasi bilan bayon qilinadi. Ular bilan tanishish uchun elektr va magnit maydon oqimi tushunchalarini aniqlab olish zarur. Eng osoni buni rasmda ko’rsatilgan S yuzadan o’tayotgan suyuqlik oqimiga o’xshashligidan foydalanib qilish lozim. Ma’lumki, 1 s da S yuzaga undan
) ma’lum bo’lsa, u holda hammaga ma’lum qoida bo’yicha harakatlanuvchi zaryadga ta’sir etuvchi kuchlarni (yoki elektr tokni) hisoblash mumkin va shuning uchun harakatlanuvchi zaryadlarning o’zaro ta’sirini hisoblash masalasi elektromagnit maydonni hisoblashga keltiriladi. Elektrodinamikada elektromagnit maydon J. Maksvellning to’rtta tenglamasi bilan bayon qilinadi. Ular bilan tanishish uchun elektr va magnit maydon oqimi tushunchalarini aniqlab olish zarur. Eng osoni buni rasmda ko’rsatilgan S yuzadan o’tayotgan suyuqlik oqimiga o’xshashligidan foydalanib qilish lozim. Ma’lumki, 1 s da S yuzaga undan 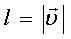 masofadan berida joylashgan suyuklik zarralari yetib keladi; bu vaqt ichida yuzadan o’tgan suyuqlik hajmi
masofadan berida joylashgan suyuklik zarralari yetib keladi; bu vaqt ichida yuzadan o’tgan suyuqlik hajmi  ga teng. Agar suyuqlikni emas, balki zaryadlangan zarralar oqimini (elektr tokni) ko’rsak, u holda 1 s da yuzachadan o’tayotgan zaryad oqimi tok kuchi bo’lib, u
ga teng. Agar suyuqlikni emas, balki zaryadlangan zarralar oqimini (elektr tokni) ko’rsak, u holda 1 s da yuzachadan o’tayotgan zaryad oqimi tok kuchi bo’lib, u 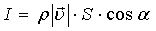 ga teng, bu yerda
ga teng, bu yerda 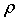 – zaryad zichligi (oqimdagi hajm birligida). Endi taqqoslashdan elektr maydon oqimi
– zaryad zichligi (oqimdagi hajm birligida). Endi taqqoslashdan elektr maydon oqimi
va magnit maydon oqimi
ni rasmiy aniqlash mumkin. Agar magnit maydon va elektr maydon yuzachadagi nuqtadan nuqtagacha o’zgarib tursa, oqimlar uchun chiqarilgan ifodalarda, xuddi suyuqlikdagidek, 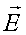 va
va 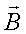 ning yuzachadagi o’rtacha qiymatlari qo’yiladi.
ning yuzachadagi o’rtacha qiymatlari qo’yiladi.
Maksvellning birinchi tenglamasini yozamiz:
bu yerda 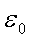 – elektr doimiysi deb ataladigan konstanta.
– elektr doimiysi deb ataladigan konstanta.
Biror hajmni o’rab turuvchi biz tanlab olgan sirtning ichida zaryadlarning joylashishini qanchalik o’zgartirmaylik, bu sirtdan o’tayotgan elektr maydon oqimi o’zgarmay qoladi. Elektrostatikada bu tenglama Gauss teoremasi deyiladi. Bu Kulon qonuniga ekvivalentdir. Lekin Kulon qonunidan farqli Gauss teoremasi umumiy hol uchun – zaryadlar harakatlanganda ham o’rinli.
Maksvellning ikkinchi tenglamasi M. Faradey ochgan elektromagnit induksiya hodisasini bayon qiladi. Agar berk kontur (masalan, egiluvchan sim) bilan chegaralangan yuzadan o’tayotgan magnit maydon oqimi vaqt o’tgan sari o’zgarsa, u holda bu konturda 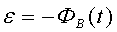 ga teng induksiya EYK hosil bo’ladi (Bu yerda
ga teng induksiya EYK hosil bo’ladi (Bu yerda 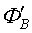 –magnit oqimning vaqt bo’yicha olingan hosilasi). Magnit maydon oqimi ifodasi uchta ko’paytuvchi
–magnit oqimning vaqt bo’yicha olingan hosilasi). Magnit maydon oqimi ifodasi uchta ko’paytuvchi 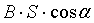 ni o’z ichiga oladi va konturdan o’tayotgan oqimning biron-bir sababga ko’ra vaqt bo’yicha o’zgarishi butkul ahamiyatsizdir: magnit maydon, kontur yuzasi yoki uning vaziyati, ya’ni
ni o’z ichiga oladi va konturdan o’tayotgan oqimning biron-bir sababga ko’ra vaqt bo’yicha o’zgarishi butkul ahamiyatsizdir: magnit maydon, kontur yuzasi yoki uning vaziyati, ya’ni 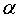 burchak o’zgaradimi – bari bir natija bir xil bo’ladi. Konturning o’tkazuvchan bo’lishi talab qilinmaydi; bu faraz qilinayotgan istalgan kontur bo’lishi mumkin. Bu kontur o’rniga o’tkazgich joylashtirilsa – bu boshqa ish. O’tkazgich bo’ylab EYK ta’sirida elektr tok oqadi. Induksiya EYK – bu elektr maydonning birlik musbat zaryadni yopiq kontur bo’yicha ko’chirishda bajargan ishiga, ya’ni kontur bo’ylab zaryadga ta’sir etayotgan o’rtacha kuchning kontur uzunligi l ga ko’paytmasiga teng. Biroq yakka musbat zaryadga ta’sir etayotgan kuch kuchlanganlik vektorining tashkil etuvchisi konturi bo’yicha urinmaga teng. Agar bu tashkil etuvchini
burchak o’zgaradimi – bari bir natija bir xil bo’ladi. Konturning o’tkazuvchan bo’lishi talab qilinmaydi; bu faraz qilinayotgan istalgan kontur bo’lishi mumkin. Bu kontur o’rniga o’tkazgich joylashtirilsa – bu boshqa ish. O’tkazgich bo’ylab EYK ta’sirida elektr tok oqadi. Induksiya EYK – bu elektr maydonning birlik musbat zaryadni yopiq kontur bo’yicha ko’chirishda bajargan ishiga, ya’ni kontur bo’ylab zaryadga ta’sir etayotgan o’rtacha kuchning kontur uzunligi l ga ko’paytmasiga teng. Biroq yakka musbat zaryadga ta’sir etayotgan kuch kuchlanganlik vektorining tashkil etuvchisi konturi bo’yicha urinmaga teng. Agar bu tashkil etuvchini 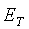 bilan belgilansa va Faradey qonunidagi
bilan belgilansa va Faradey qonunidagi 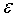 ni
ni 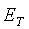
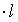 ga almashtirilsa, Makevellning ikkinchi tenglamasi kelib chiqadi:
ga almashtirilsa, Makevellning ikkinchi tenglamasi kelib chiqadi:
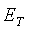
|
X l | 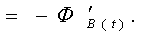 (2) (2) |
| Tashkil etuvchi-ning konturiga o’tkazilgan urinmaning o’rtacha qiymati | Kontur uzunligi | Kontur bilan chega-ralangan yuzadan o’ta-yotgan oqim |
Elektrostatikada tenglamaning (2) o’ng tomoni nolga aylanadi, bu elektr kuchlarining zaryadi istalgan yopiq kontur bo’yicha ko’chirishda bajargan ishi ham nolga teng ekanligini bildiradi.
Elektr maydonning elektrostatikaga elektr potentsialni kiritishga imkon yaratgan bu ajoyib hususiyati o’zgaruvchan magnit maydon paydo bo’lishi bilan yo’qoladi. O’zgaruvchan magnit maydon uyurma elektr maydonni hosil qiladi, uning kuch chiziqlari aniq bo’ladi va yopiq konturda bajargan ishi nolga teng bo’lmaydi. Umumiy holda to’liq elektr maydon elektr zaryadlari hosil qilgan maydon va o’zgaruvchan magnit maydon hosil qiladigan uyurma elektr maydon yig’indisidan iborat. Elektromagnit induksiya hodisasi elektr stantsiyalarida elektr toki generatorlari ishining asosini tashkil etadi, fizik tadqiqotlarda esa uyurma elektr maydonlardan, zaryadlangan zarralar tezlatgichlarida foydalaniladi.
Maksvell tenglamalari ikkinchi jufti magnit maydonlarni ifodalaydi;
| FB | =0 (3) |
| Istalgan yopiq sirtdan o’tayotgan magnit maydon oqimi |
Maksvellning uchinchi tenglamasi tabiatda magnit zaryadlarning mavjud emasligini aks ettiradi. Elektrostatikadan ma’lumki, elektr maydonning kuch chiziqlari musbat zaryadlardan boshlanadi na manfiy zaryadlarda tugaydi. Agar biz magnit maydonning kuch chiziqlarini o’tkazsak, ular doimo berk bo’ladi yoki cheksizlikka intiladi. Demak, qancha kuch chiziqlari yopiq, ya’ni chegaralangan hajm, sirt ichiga kirsa, shunchasi undan chiqadi va shuning uchun yopiq sirtdan o’tayotgan magnit maydonning to’liq oqimi har doim nolga teng bo’ladi.
Magnit maydonni harakatlanuvchi zaryadlar, ya’ni elektr tok hosil qiladi va bu hodisa Maksvellning to’rtinchi tenglamasi bilan ifodalanadi. Uni avval magnitostatikada qanday ifodalansa, shunday yozamiz (magnitostatika– elektrodinamikaning o’zgarmas elektr toklari hosil qilgan magnit maydonni o’rganuvchi bo’limi). Xuddi ikkinchi tenglamadagidek, u ixtiyoriy yopiq kontur uchun yoziladi, faqat elektr maydon kuchlanganligi tashkil etuvchisining konturiga urinma o’rnida tenglamaning o’ng qismida BT induksiya vektori tashkil etuvchisining urinmasi bo’ladi:
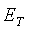
|
X l | 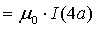 |
| Vektor tashkil etuvchisi konturiga o’tkazilgan urinma o’rtacha qiymati | Kontur uzunligi | Kontur bilan chegaralangan yuzadan o’tayotgan elektr toki |
Bu yerda μ0 – magnit doimiysi deb ataladigan konstanta.
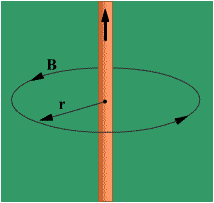
Tokli to’g’ri o’tkazgich magnit maydonni hosil qiladi, uning kuch chiziqlari markazi o’tkazgich o’qida joylashgan kontsentrik aylanalarni ifodalaydi. (4a) tenglama yordamida o’tkazgichdan r masofadagi magnit maydon kattaligini hisoblash uchun kuch chiziqlari bilan mos keladigan konturni tanlaymiz. U holda 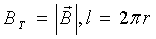 va (4a)
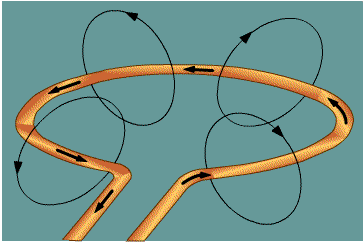
va (4a) 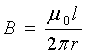 tenglamadan kelib chiqadi. Xuddi shunday tokli ramkadagi kuch chiziqlari rasmda ifodalangan magnit maydonni ham hisoblash mumkin (lekin buni qilish murakkab). Tokning magnit maydoni ramkadagi tok kuchi l ga, demak, ramkaning xususiy magnit maydoni ham l ga proportsional bo’ladi:
tenglamadan kelib chiqadi. Xuddi shunday tokli ramkadagi kuch chiziqlari rasmda ifodalangan magnit maydonni ham hisoblash mumkin (lekin buni qilish murakkab). Tokning magnit maydoni ramkadagi tok kuchi l ga, demak, ramkaning xususiy magnit maydoni ham l ga proportsional bo’ladi: 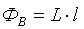 . Proportsionallik koeffitsiyenti L ramkaning induktivligi deyiladi. Agar ramkadagi tok vaqt o’tgan sari o’zgarib tursa, u holda xususiy magnit maydoni oqimi ham o’zgaradi, demak ramkada
. Proportsionallik koeffitsiyenti L ramkaning induktivligi deyiladi. Agar ramkadagi tok vaqt o’tgan sari o’zgarib tursa, u holda xususiy magnit maydoni oqimi ham o’zgaradi, demak ramkada 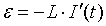 ga teng induksiya EYUK hosil bo’ladi. Bu hodisaga o’zinduktsiya deyiladi. Oxirgi munosabatning o’ng qismidagi « – » belgisi (2-tenglamadagidek) Lens qoidasini ifodalaydi: induksiya EYK har doim konturdan o’tayotgan magnit oqimi o’zgarishiga to’sqinlik qiladi.
ga teng induksiya EYUK hosil bo’ladi. Bu hodisaga o’zinduktsiya deyiladi. Oxirgi munosabatning o’ng qismidagi « – » belgisi (2-tenglamadagidek) Lens qoidasini ifodalaydi: induksiya EYK har doim konturdan o’tayotgan magnit oqimi o’zgarishiga to’sqinlik qiladi.
Yuqorida o’zgaruvchan magnit maydon uyurma elektr maydonni (elektromagnit induksiya hodisasini) vujudga keltirishi gapirildi. Maksvell magnit maydonni faqat elektr toklarigina emas, balki o’zgaruvchan elektr maydonlar ham hosil qilishini nazariy jihatdan avvaldan aytib berdi. Maksvell fikriga muvofiq (4a) tenglamaning o’ng tomonida elektr maydonning o’zgarish tezligiga proportsional bo’lgan qo’shimcha qo’shiluvni bo’lishi shart va M a k s v e l l ning to’rtinchi tenglamasi to’liq holda quyidagicha ifodalanadi:
bu yerda FE –ixtiyoriy konturdan o’tayotgan elektr maydon oqimi.
Agar o’zgaruvchan elektr maydon magnit maydonni hosil qilsa, o’zgaruvchan magnit maydon ham elektr maydonni hosil qiladi, demak, elektromagnit maydon zaryadlar bo’lmaganda ham mavjud bo’lishi mumkin. Elektromagnit maydon vakuumda elektromagnit to’lqinlar ko’rinishida mavjud bo’lib, ular 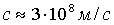 tezlik, ya’ni yorug’lik tezligi (yorug’lik ham elektromagnit to’lqindir) bilan tarqaladi. Elektromagnit to’lqinlar energiya va impulsga ega; demak, elektromagnit maydon bu zaryadlarning o’zaro ta’sirini bayon qilish usuli bo’lmay, balki zaryadlar va elektr tok singari fizik reallikdir. Birinchi marta G. Gers tajribada kuzatgan elektr to’lqinlarining mavjudligini J. Maksvellning nazariy farazlari a’lo darajada tasdiqladi.
tezlik, ya’ni yorug’lik tezligi (yorug’lik ham elektromagnit to’lqindir) bilan tarqaladi. Elektromagnit to’lqinlar energiya va impulsga ega; demak, elektromagnit maydon bu zaryadlarning o’zaro ta’sirini bayon qilish usuli bo’lmay, balki zaryadlar va elektr tok singari fizik reallikdir. Birinchi marta G. Gers tajribada kuzatgan elektr to’lqinlarining mavjudligini J. Maksvellning nazariy farazlari a’lo darajada tasdiqladi.
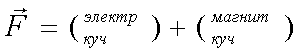
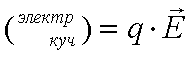

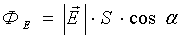
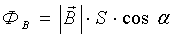
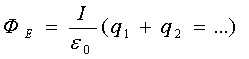 (1)
(1)
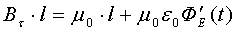 (4)
(4)