Qaralayotgan sistemaning barcha nuqtalari tanlangan sanoq sistemasiga nisbatan tinch turadigan holatiga mexanik sistemaning muvozanati deyiladi.

Muvozanat shartlarini eng sodda mexanik sistema - moddiy nuqta misolida aniqlash hammadan ham soddadir. Dinamikaning birinchi qonuniga muvofiq (Mexanika). moddiy nuqtaning inersial koordinatalar sistemasida tinch holatda (yoki tekis to’g’ri chiziqli harakatda) bo’lishi sharti unga ta’sir etuvchi barcha kuchlar vektor yig’indisining nolga teng bo’lishidir.

Murakkabroq mexanik sistemalarga o’tganda ularning muvozanati uchun birgina bu shart kifoya qilmaydi. Murakkab mexanik sistemaning muvozanatlanmagan tashqi kuchlar ta’sirida ilgarilanma harakat qilishidan tashkari aylanma harakat qilishi yoki deformatsiyalanishi mumkin.

Absolyut qattiq jism – o’zaro masofasi o’zgarmaydigan zarralar to’plamidan iborat mexanik sistemaning muvozanatda bo’lish shartlarini aniqlaylik.

Moddiy nuqta uchun qilinganidek, mexanik sistemaning barcha nuqtalariga ta’sir etayotgan kuchlar yig’indilari nolga teng bo’lsin, deb talab qilib, mexanik sistemaning ilgarilanma (tezlanishli) harakati imkoniyatini bartaraf qilish mumkin. Shuning o’zi mexanik.sistema muvozanatining birinchi shartidir.

Bizning holda qattiq jism deformatsiyalanishi mumkin emas, chunki biz uning nuqtalari orasidagi masofa o’zgarmaydi, deb kelishib olganmiz. Lekin moddiy nuqtadan farqli ravishda absolyut qattiq jismning turli nuqtalariga teng va qarama-qarshi yo’nalgan kuchlar juftini ta’sir qildirish mumkin. Bunda bu ikki kuch yig’indisi nolga tengligi tufayli qaralayoggan mexanik sistema ilgarilanma harakat qila olmaydi. Biroq shunday kuchlar jufti ta’sirida jism biror o’q atrofida ortib boruvchi burchak tezlik bilan aylana boshlaydi.

Qaralayotgan sistemada aylanma harakatning vujudga kelishiga sabab muvozanatlanmagan kuchlar momentlarining mavjudligidir. Biror o’qqa nisbatan kuch momenti deb bu F kuchning d yelkaga, ya’ni o’q o’tgan O nuqtadan kuch yo’nalishiga tushirilgan perpendikulyarning uzunligiga (rasmga q.) ko’paytmasiga aytiladi. Bunday ta’rifga muvofiq kuch momenti algebraik kattalik bo’lishini ta’kidlaymiz: agar kuch soat strelkasiga qarshi aylanishga olib kelsa, uni musbat deb, aksincha bo’lsa manfiy deb hisoblanadi. SHunday qilib, barcha kuchlarning har qanday aylanish o’qiga nisbatan momentlari yig’indisi nolga teng bo’lishi talabi - qattiq jism muvozanatining ikkinchi shartidir.

Topilgan ikkala muvozanatlik shartlari bajarilgan holda, agar kuchlar ta’sir qila boshlagan paytda qattiq jismning barcha nuqtalari tezliklari nolga teng bo’lsa, shu qattiq jism tinchlik holatida turaveradi. Aks holda u inersiya tufayli tekis harakat qilaveradi.

Mexanik sistemaning muvozanatda bo’lishining qarab o’tilgan ta’rifi, agar sistema muvozanat vaziyatidan ozgina chiqsa, nima yuz berishi haqida hech narsa demaydi. Bu holda uch imkonnyat bor: sistema o’zining dastlabki muvozanat holatiga qaytadi; og’ishishga qaramasdan sistema o’z muvozanat vaziyatini o’zgartirmaydi; sistema muvozanat holatidan chiqib ketadi. Birinchi holni turg’un muvozanat holati, ikkinchisini farqsiz, uchinchisini turg’unmas muvozanat holati deyiladi. Muvozanat holati xarakteri sistema potensial energiyasining koordinatlarga bog’lanishi bilan aniqlanadi. Rasmda chuqurda turgan (turg’un muvozanat), silliq gorizontal stol ustida turgan (farqsiz muvozanat), do’nglik cho’qqisida turgan (turg’unmas muvozanat) og’ir sharcha misolida muvozanatning barcha uch tipi ko’rsatilgan.

Yuqorida bayon qilingan mexanik sistemaning muvozanati muammosini olimlar kadim zamonlardayoq tekshirganlar. Masalan, richag (ya’ni mahkamlangan aylanish o’qiga ega bo’lgan qattiq jism) ning muvozanat qonunini Arximed eramizdan oldingi III asrda topgan.

1717 yilda Iogann Bernulli mexanik sistemaning muvozanati shartlarini topishning mutlaqo boshqacha usulini-virtual ko’chishlar metodini ishlab chiqdi. Uning asosida energiyaning saqlanish qonuni kelib chiqadigan bog’lanishlar reaktsiyasi kuchlari xossasi yotadi: sistema muvozanat vaziyatidan ozgina og’ishgan holda bog’lanishlar reaktsiyasi kuchlarining to’la ishi nolga teng bo’ladi.

Statika (Mexanika) masalalarini yuqorida ta’riflangan muvozanat shartlari asosida yechishda sistemada mavjud bo’lgan bog’lanishlarii (tayanchlar, iplar, sterjenlarni) ularda paydo bo’ladigan reaktsiya kuchlari xarakterlaydi. Bir qancha jismlardan tarkib topgan sistemalar holida bu kuchlarii hisobga olish zarurati juda katta hisoblashlarga olib keladi. Biroq muvozanat holatidan ozgina og’ishlar holida bog’lanishlar reaktsiyasi kuchlarining ishi nolga teng bo’lishi tufayli bu kuchlarni umuman tekshirmaslik mumkin.

Mexanik sistemaning nuqtalariga reaktsiya kuchlaridan boshqa tashqi kuchlar ham ta’sir qiladi. Muvozanat holatidan ozgina og’ishish holida ular qanday ish bajaradi? Sistema dastlab tinch turgani sababli uning har qanday ko’chishi uchun biror musbat ish bajarish zarur. Umuman bu ishni tashqi kuchlar ham, bog’lanishlar reaktsiyasi kuchlari ham bajarishi mumkin. Lekin reaktsiya kuchlarining to’la ishi nolga teng bo’lishini bilamiz. SHu sababdan sistemaning muvozanat holatidan chiqib ketishi uchun mumkin bo’lgan har qanday ko’chishda tashqi kuchlarning natijaviy ishi musbat bo’lishi kerak. Binobarin, harakatning mumkinmasligi sharti, ya’ni muvozanat shartini mumkin bo’lgan har qanday ko’chishda tashqi kuchlarning to’la ishi musbat bo’lmasligi kerak: ΔA≤0 degan talab tarzida ifodalash mumkin.

Faraz qilaylik, sistema nuqtalarining 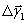,…, 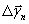ko’chishlarida tashqi kuchlar ishlari yig’indisi A1 bo’lsin. Agar sistema -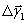, - ,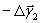…,- 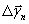ko’chishlar bajarsa, u holda nima yuz boradi? Oldingi ko’chishlar singari, bu ko’chishlar ham bo’lishi mumkin; biroq endi tashqi kuchlar ishi ishorasi o’zgaradi: ΔA₂ = ΔA₁ oldingi holdagi kabi mulohaza yuritib, endi sistemaning muvozanat sharti ΔA₁≥0 ko’rinishini oladi, ya’ni tashqi kuchlar ishi manfiy bo’lmasligi kerak, degan xulosaga kelamiz. Deyarli bir-biriga zid bo’lgan bu ikki shartni «kelishtirish» ning yagona imkoniyati - sistemaning muvozanat vaziyatidan har qanday imkonli (virtual) ko’chishida tashqi kuch­larning to’la ishi aniq nolga teng, ya’ni ΔA=0 bo’lishini talab qilishdir. Imkonli (virtual) ko’chish deganda, bu yerda sistemaning undagi bog’lanishlarga zid kelmaydigan cheksiz kichik faraz qilingan ko’chishi tushuniladi.

Demak, mexanik sistemaning virtual ko’chishlar prinsipi ko’rinishidagi muvozanat sharti quyidagi tarzda ifodalanadi:

«Ideal bog’lanishlarga ega bo’lgan har qanday mexanik sistemaning muvozanatda bo’lishi uchun har qanday imkonli ko’chishda sistemaga ta’sir qilayotgan kuchlar elementar ishlari yig’indisi nolga teng bo’lishi zarur va kifoyadir».

Virtual ko’chishlar printsipi yordami bilan faqatgina statika masalalari emas, balki gidrostatika va elektrostatika masalalari ham hal qilinadi.