Figurachilarning muz maydonida chiqishlarini jozibali tugallashlarini hayratlanish va zavq bilan kuzatmagan biron kimsa bormikan? Ular bitta konkilarini aylanish markaziga qo’yib, qo’llarini keng yoyganlaricha ikkinchi konkilari bilan itarilib, anchagina katta burchak tezlikda aylanishga erishadilar va keyin tezgina qo’llarini tanalariga yopishtirib oladilar. Shundan so’ng ularning aylanish burchak tezligi keskin ortadi.

Buning sababi nimada? Faqat qo’llarini tanasiga yopishtirib va hech qanday qo’shimcha kuch sarflamay figurachi o’z aylanish burchak tezligini qanday qilib keskin oshirishga erishadi? Bu bilan energiyaning saqlanish qonuni buzilmaydimi? Albatta, yo’q. Tavsiflangan hodisani Nyuton mexanikasining bo’limlaridan biri-qattiq jism dinamikasi tushuntirib beradi. Bunda qattiq jism deganda o’zaro masofalari o’zgarmaydigan zarralar sistemasi tushuniladi.

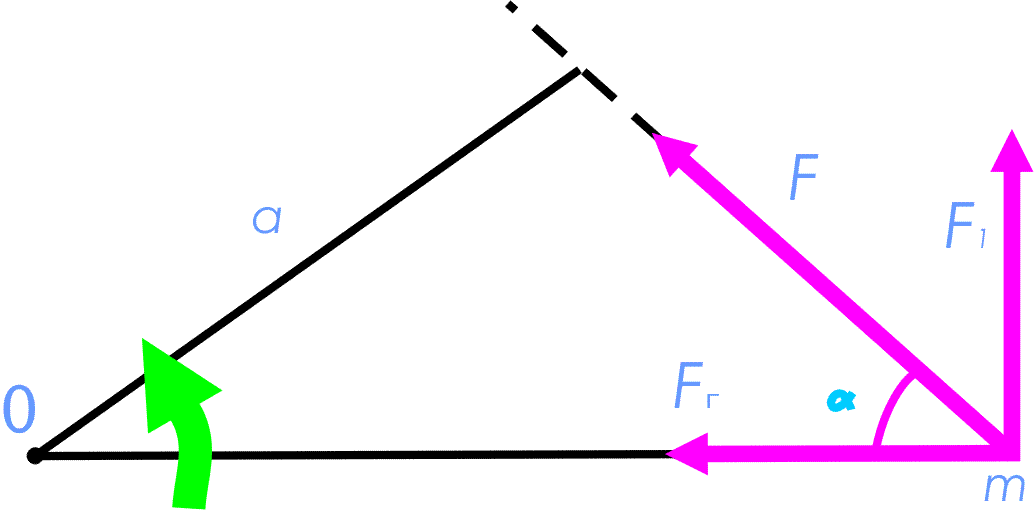
Qattiq jismning aylanma harakatiga oid masalaning murakkabligiga qaramay, uni shakli jihatdan ilgarilanma harakat uchun Nyuton tenglamalariga o’xshash tenglamalarni yechishga keltirish mumkin ekan. Bu holda tezlanish, kuch va massa rolini ushbu holda burchak tezlik, kuch momenti va inersiya momenti o’taydi. Bu muhim tushunchalar bilan r radiusli aylanada vaznsiz sterjen yordamida tutib turilgan m> massali bitta A> moddiy nuqtaning harakatidan iborat oddiy misolda tanishish mumkin. Aytaylik, A> nuqtaga 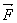doimiy kuch ta’sir qilayotgan bo’lsin. Agar ushbu paytda u A> moddiy nuqtaning radius-vektori bilan α burchak hosil qilayotgan bo’lsa, u holda uning 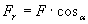tashkil etuvchisi bevosita sterjenni qisadi, 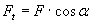tashkil etuvchisi esa zarra tezligi kattaligini o’zgartiruvchi αt tangentsial tezlanish hosil bo’lishiga olib keladi. Bu tezlanish zarra traektoriyasiga urinma bo’yicha yo’nalgan. Uni hamma vaqt aylanish markaziga tomon yo’nalgan hamda zarra tezligi vektorining yo’nalishinigina o’zgartiradigan markazga intilma tezlanishdan farq qilish lozim.

Nyutonning ikkinchi qonuniga ko’ra, tangentsial tezlanish uchun quyidagini yozish mumkin: ma_t=F_t=F•cosα(1)

Burchak tezlikka o’xshash tarzda 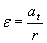burchak tezlanishi kiritamiz. U burchak tezligi ω ning vaqt o’tishi bilan o’zgarish tezligini xarakterlaydi. U holda (1) tenglik quyidagi ko’rinishni oladi: 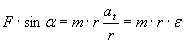(2)

Bu tenglamaning ikkala qismini radiusga ko’paytirib, quyidagini hosil qilamiz: F•r•sinα=mr²ε, (3) yoki M=J•ε

Son qiymati jihatidan F kuchning kuch yo’nalshiga aylanish markazidan tushirilgan d=r•sinα perpendikulyar (kuch yelkasi) uzunligiga ko’paytmasiga teng bo’lgan M=F•r•sinα kattalikni O nuqtaga nisbatan kuch momenti deyiladi. A moddiy nuqta massasining uning aylanish markazigacha masofani kvadratiga ko’paytmasiga teng bo’lgan F=m•r² kattalikka moddiy nuqtaning O nuqtaga nisbatan inersiya momenti deyiladi.

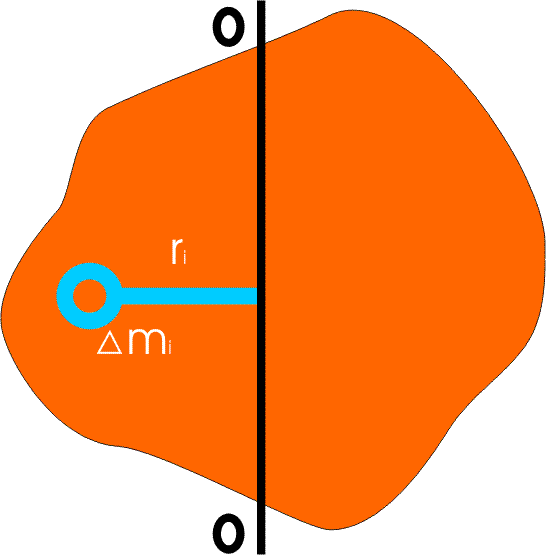
Ixtiyoriy qattiq jism holida inersiya momenti shu jismdagi massasining taqsimoti bilan xarakterlanadi hamda qattiq jismni ajratish mumkin bo’lgan moddiy nuqtalar majmuasining inersiya momentlari yig’indisi bilan aniqlanadi: 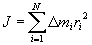(4) bunda Δm_i-i-nuqta massasi, r_i-uning aylanish o’qigacha masofasi.

Inersiya momenti jismning aylanish vaqtidagi inertlik o’lchovi hisoblanadi va demak, ilgarilanma harakatdagi massa kabi rolni bajaradi. Biroq odatdagi sharoitlarda o’zgarmay qoladigan jismning massasidan farqli ravishda, inersiya momentini oson o’zgartirish mumkin. haqiqatdan ham, hatto yuqorida qaralgan, sterjendagi moddiy nuqtadan iborat oddiy holda ham inersiya momenti faqat massa kattaligigagina emas, balki uning aylanish o’qidan uzoqlashtirish yo’li bilan bunday sistemaning aylanish inersiyasini kattalashtirish mumkin.

Shakliga hamda tanlangan aylanish o’qiga qarab, bir xil massali qattiq jismlar turli inersiya momentlariga ega bo’lishi mumkin. Masalan, k radiusli kavak tsilindrning uning simmetriya o’qiga nisbatan inersiya momenti mr² ga; markazidan o’tuvchi o’qqa nisbatan aylanayotgan bir jinsli tsilindrniki 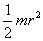ga teng.

Kuch momenti 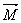ham, burchak tezlik 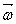ham, burchak tezlanish 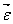ham, ilgarilanma harakatni tavsiflashdagi ularga mos kattalikdar-kuch, tezlik va tezlanishlar kabi, vektor kattaliklardir. Bu vektorlar aylanish o’qi bo’yicha bo’yicha yo’nalgan bo’lib (aksial vektorlar), ularning yo’nalishi pparma qoidasi bo’yicha aniqlanadi, ya’ni dastasi jism kabi yo’nalishda aylanayotgan parmaning ilgarilanma harakatiga to’g’ri keladi.

Yana bitta muhim vektor 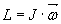kiritish mumkin: unga harakat miqdori momenti deyiladi. U aylanma harakatdagi impulsga o’xshash bo’lib ajoyib xossaga ega: yopiq sistemaning harakat miqdori momenti kattaligi va yo’nalishi bo’yicha doimiy qoladi. U qaralayotgan sistemaga qo’yilgan tashqi kuchlarning kompensatsiyalanmagan momenti ta’siridagina o’zgarishi mumkin.

Ushbu maqolaning aylanayotgan figurachi haqida hikoya qilingan boshlanishiga qaytaylik. Unga ta’sir qilayotgan kichik qarshilik kuchlari momentlarini nazarga olmasak, u yopiq sistemani hosil qiladi, deyish mumkin. Shuning uchun u boshida erishgan harakat miqdori momenti saqlanishi lozim 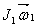( 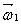-uning boshlang’ich burchak tezligi, J₁-uning qo’llar yoyilgan holdagi inersiya momenti). Figurachi qo’llarini tanasiga yopishtirib, ravshanki, o’zining inersiya momentini biror J₂ kattalikkacha kamaytiradi va bu bilan o’zining burchak tezligini oshiradi: 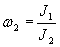. Biroq uning boshlang’ich aylanish kinetik energiyasi 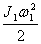, oxirgisi esa 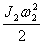bo’lgani uchun unga bu paytda «ishlashga» to’g’ri keladi. Bu energiyalar farqi figurachi ishi kattaligini tashkil qiladi.