Protsesslarning yo’nalishini avvaldan aytib berish imkoni termodinamika ikkinchi qonunining asosiy mazmunini tashkil etadi. Nemis fizigi R. Klauzius protsessning bir tomonlama kechishiga olib keluvchi cheklashni tahlil qilib S funksiyani kiritdi va uni entropiya deb atadi. Klauzius ta’rifida (1865) termodinamikaning ikkinchi qonuni shunday ifodalanadi:"O’zgarmas energiyaga ega sistemalarda o’z-o’zicha kechadigan protsesslarda entropiya hamisha o’sib boradi".

Shunday qilib, agar S_B>S_A bo’lsa, sistema, o’z-o’zicha A sharoitdan V sharoitga o’tadi. Aks holda: S_B>S_A teskari protsess o’z-o’zicha kechadi. Entropiyaning qizish, sovish, erish, bug’lanish, ximiyaviy reaktsiyalar va shu kabilar bilan bog’liq bo’lgan turli protsesslarda o’zgarishini hisoblashning umumiy usullari mavjud. Hisoblashning bu usullari, retseptlari termodinamikaning ajralmas qismini tashkil etadi va ularning hammasi u yoki bu tajriba natijalaridan foydalanishga asoslanadi.

Masalan, entropiyaning erishda o’zgarishi ΔS_er ni hisoblash uchun erish issiqligi λ ni erish temperat urasi T_er ga bo’lish kerak. 1 mol (18g) muzni eritish uchun λ=6,02kJ/mol, T_er=273K bo’lishi kerak; mos holda =22 J/mol • grad. Suvning entropiyasi muzning entropiyasidan katta.

ΔS_er=22J/mol gradgrad. Suvning entropiyasi muzning entropiyasidan katta.

Avstriya fizigi L. Bolsman entropiyaning fizik ma’nosini va uning izolyatsiyalangan sistemalarda (o’zgarmas energiyaga ega sistemalar shunday ataladi) o’sib borishi sabablarini aytib berdi. Bolsman fikriga ko’ra, entropiya sistemadagi tartibsizlik o’lchovidir. To’liq tartib entropiyaning minimum qiymatiga to’g’ri keladi; har qanday tartibsizlik uni o’stiradi. Shunday qilib, entropiya o’sishining fizik ma’nosi quyidagicha: zarralar to’plami tashqi ta’sirlarni sinamay (izolyatsiyalangan sistema) o’z-o’zicha qolish imkoniyati yaratilsa, bu zarralar tartibsizligi juda yuqori bo’lgan holatga o’tadi. Maksimal entropiya to’liq betartiblikka mos keladi.

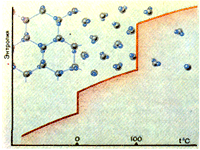
O’zimizdan so’raylik: atomlar qaerda tartibli joylashadi – kristall panjarasida atomlar malum vaziyatni (tugunlarni) egallagan kristall kattiq jismdami yoki atomning malum, mustahkam holati bo’lmagan suyuqlikdami? Javob aniq: qattiq jismda. Modomiki entropiya – tartibsizlik o’lchovi ekan, u suyuqlikda kristaldagiga nisbatan katta; avval aytib o’tilganidek, suv entropiyasi muz entropiyasidan kattadir. Endi zarralar holatini suv bug’ida va suvda solishtiraylik. Molekulalarning vaziyatlari unda ham, bunda ham qayd qilinmagan. Lekin uy temperaturasida va atmosfera bosimida 1 mol suv (18 g) 18 sm³ hajmni egallaydi (suvning zichligi 1 g/sm³), 1 mol suv bug’i esa – 22,4 l ni, ya’ni 1000 marta katta hajmni egallaydi. Qayerda tartibsizlik katta bo’ladi. Albatta, bunda haqiqatan ham, bug’ entropiyasi suv entropiyasidan kattadir, shuni ham aytish kerakki, uning bug’lanishdagi o’zgarishi erishdagi o’zgarishiga qaraganda 5 marta katta:ΔS_bulg=108J/mol • grad. Entropiyaning maksimum mezoni faqat izolyatsiyalangan jismlar uchungina to’g’ri. Aks holda barcha jismlar gaz bo’lishi kerak edi. Agar jism atrof-muhit bilan issiqlik almashsa, u holda Gibbs fikriga ko’ra, turg’un holatga boshqa termodinamik funktsiyalarning eng kichik qiymati to’g’ri keladi (Issiqlik muvozanati). Xuddi shuning uchun erish temperaturasidan pastda qattiq holat, erish va qaynash temperaturalari oralig’ida suyuq holat bo’ladi va hokazo.

Bolsman birinchi bo’lib, «sistemaning holatlari ehtimolliklari» yoki ma’lum bir holatni amalga oshirishga yordamlashadigan usullar sonini ifodalaydigan termodinamik iborani kiritdi. Bolsman fikriga muvofiq molekulalarning o’zaro to’qnashuvlari natijasida sistemada molekulalar tezliklari va koordinatlarining turli kombinatsiyalari vujudga kelishi mumkin, ular sistema holatini mexanik nuqtai nazardan o’zgartirmaydi (sistema energiyasi o’zgarmaydi), lekin termodinamik nuqtai nazardan sistema holati o’zgaradi. Juda ko’p zarralardan tashkil topgan har qanday sistema ehtimolligi kamroq holatdan juda ko’p usullar bilan amalga oshadigan ehtimolligi ko’proq holatga o’tadi.

Entropiya S va berilgan holatni amalga oshiradigan usullar soni (termodinamik ehtimollik) R orasidagi bog’lanishni mashhur Bolsman formulasi beradi: S=klnp+const, bu yerda ,k=1,38•10^-23J/grad– Bolsman doimiysi.