Sistema holatining o’zgarishida moddaning bir fazadan boshqasiga o’tishi fazaviy o’zgarishlar deyiladi. Faza muayyan ximiyaviy tarkibga va termodinamik xossalarga ega bo’lgan, boshqa fazalardan bo’linish sirti bilan ajralgan moddiy ob’ektlar majmuasi. Yoki boshqacha aytganda, faza – bir jinsli bo’lmagan sistemaning bir jinsli qismi bo’lib, u sistemadan biror-bir mexanik usul bilan ajratilishi mumkin. Odatda, bitta gaz faza mavjuddir (gaz aralashmalarining juda yuqori bosimlarda kamdan-kam uchraydigan qatlamlanish hollarini istisno qilganda). Suyuq va ayniqsa, qattiq fazalar g’oyat ko’p bo’lishi mumkin.

Fazaviy o’zgarishlarning asosiy xarakteristikasi – fazalar termodinamik muvozanat holatida bo’ladigan temperatura bo’lib, unga fazaviy o’tishlar nuqtasi deyiladi. Niderlandiyadagi Leyden universiteti professori P. Erenfest 1933 yilda fazaviy o’tishlar klassifikatsiyasini taklif qildi. Bu klassifikatsiiga ko’ra, birinchi tur fazaviy o’tishlar uchun fazaviy o’tishlar nuqtasida issiqlik (q) ning ajralishi yoki yutilishi hamda hajmning o’zgarishi (Δv ) kuzatiladi. Birinchi tur fazaviy o’tishlarga, masalan, qattiq jismning suyuqlikka aylanishi (erish) va teskari protsess kristallanish(), suyuqlikning bug’ga aylanishi (bug’lanish, qaynash), bir kristall modifikatsiyadan boshqasiga o’tish (polimorf o’zgarishlar) va boshqalar kiradi.

Ikkinchi tur fazaviy o’tishlarda issiqlik va hajmiy effektlar bo’lmagani holda, o’tish nuqtasida issiqlik sig’imning, issiqlik kengayish, siqiluvchanlik hajmiy koeffitsiyentlarining o’zgarishi kuzatiladi.

Masalan, normal o’tkazgichning o’ta o’tkazuvchan (O’ta o’tkazuvchanlik), geliyning o’ta oquvchan geliy 11 (O’ta oquvchanlik), ferromagnetikning paramagnetik (Magnetizm) holatga o’tishi va ikqinchi tur fazaviy o’tishlarga misol bo’la oladi.

Fazaviy muvozanat holatida fazaviy o’zgarish temperaturasi bilan bosim orasida muayyan bog’lanish mavjud. Masalan, erish yoki qaynash temperaturasi tashqi bosimga bog’liq , to’yingan bug’ bosimi esa berilgan temperaturada juda aniq qiymatga ega bo’ladi. Son jihatdan bu bog’lanish birinchi tur fazaviy o’tishlar uchun Klapeyron–Klauzius tenglamasi orqali ifodalanib, unga ko’ra, Δq/ΔT=q/TΔv.

Erishda issiqlik yutilganligi (q>0 ) tufayli, suyuq faza hajmi esa odatda qattiq faza hajmidan katta (Δq>0 ) bo’lganligidan, erish temperaturasi odatda, bosim ortishi bilan ko’tariladi, qotishda hajm ortishi hollari (vismut, galliy, suv, cho’yan) bundan istisnodir.

Effekt, odatda, kichik bo’lib, u 10^-2 K/atm, tartibidadir. To’yingan bug’ bosimi temperatura ko’tarilishi bilan hamma vaqt o’sib boradi.

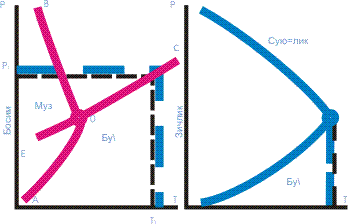
Fazaviy muvozanatni diagrammalar yordamida ifodalash qulay. Bitta moddadan, masalan, suvdan tashkil topgan eng sodda bir komponentli sistema uchun shunday diagramma keltirilgan. OA va OS chiziqlardan pastda, ya’ni past bosim va yuqori temperaturalarda bug’ning turg’unligiga mos kelgan soha joylashgan, OV va OS chiziqlar orasida suyuqlikka hamda OA va OV chiziqlar orasida qattiq muzga mos sohalar joylashgan. Bu sohalarning har biri ichida fazalardan birining turg’unlik sohasida qolgani holda, ixtiyoriy va mustaqil tarzda ikkita parametr temperatura T va bosim r ni o’zgartirish mumkin.

OA, OV va OS chiziqlar orqali tavsiflanuvchi sistema holati ikkita faza orasidagi muvozanatga, masalan, OS –suv va bug’ orasidagi muvozanatga mos keladi. Barcha uchta chiziqning kesishish nuqtasi – uchlanma nuqta deb ataladigan nuqtada uchala faza (muz, suv, bug’) muvozanatda bo’ladi. Uchlanma nuqtada temperatura va bosim aniq qiymatga ega bo’ladi (masalan, suv uchun 0,0078⁰S va 4,579 mm sim. ustuni).

1-rasmda OS chiziqning davomidan iborat bo’lgan OE punktir chiziq o’ta sovigan suv bug’i bosimining temperaturaga bog’lanishini ko’rsatadi. U, ma’lumki, muz bug’i bosimidan xamma vaqt yuqoridir. Bunday faza ancha barqaror bo’lgan faza mavjudligida beqaror () bo’ladi. Metastabil fazalar (o’ta qizish va o’ta sovush) ning mavjud bo’lish imkoniyati – birinchi tur fazaviy o’tishlarning xarakterli xususiyatidir. O’ta qizish va o’ta sovish jarayoni yangi fazalarning (muz kristalchalari, suyuqlik tomchilari, bug’ pufakchalari) hosil bo’lishi uchun energiya sarflashni taqozo qiladi. Agar bug’ va suyuqlikni boshqa fazaga o’tkazish uchun turli xil hiylalar ishlatishga to’g’ri kelsa (masalan, bug’ pufakchalari chang zarralarida oson hosil bo’ladi, demak, o’taqizigan suv g’oyat toza bo’lishi lozim), kristallar uchun esa beqaror fazalarda uzoq muddat barqaror mavjud bo’lishlik – deyarli odatga kirgan. Masalan, uy temperaturasi va atmosfera bosimida grafit bo’lishi lozim bo’lgan olmos yetarlicha barqarordir. Oq qalay 18⁰da qo’ng’ir qalay kukuni (qalay o’lati)ga aylanishi lozim. Biroq ma’lumki, u 20–30 gradusgacha o’tasovitishlarga oson bardosh beradi. Lekin har holda qahraton qish sharoitlarida qalayda o’zgarishlar sodir bo’ladi. Bu holni bilmaslik oqibatida R. Skott ekspeditsiyasi 1912 yilda Janubiy qutbda halokatga uchragan. Ekspeditsiyaning suyuq yoqilg’i zapaslari qalay bilan payvandlangan idishlarda saqlanar edi. Qattiq sovuqda idish payvandlari ochilib, yoqilg’i oqib ketgan.

Bir fazani boshka fazadan ajratuvchi bo’linish sirtida xossalar odatda sakrash bilan o’zgaradi. Masalan, suv bug’ining zichligi suvning zichligidan ancha kichikdir. Lekin, agar temperatura ko’tarilsa, ular yaqin lasha boradi va qandaydir kritik temperaturada teng bo’lib qoladi. Suyuqlik va to’yingan bug’ orasidagi fizik xossalarning farqi yo’qoladigan temperaturaga kritik temperatura deyiladi. Tegishli bosim kritik bosim deyiladi.

Kritik temperaturadan past temperaturalarda suvning bir-biridan oson farq qilinadigan ikki holati – bug’ va suyuqlik holati mavjud. Kritikdan yuqori temperaturalarda modda bir jinsli bug’ holatida bo’ladi. Agar bu bug’ egallagan hajm kichraytirilsa, bosim ortgani holda bug’ suyuqlikka aylanmaydi. Hech qanday bosimda keskin chegarali ikkita holatni (kritikdan past temperaturada bug’ning kondensatsiyasi tufayli bo’lganidek) hosil qilib bo’lmaydi.

Shu sababli, M. Faradey bosimni oshirish yo’li bilan kislorod va vodorodni uzoq vaqt kondensatsiyalay olmagan edi, ularni dastlab kritikdan pastroq temperaturagacha sovitish lozim edi.

Har bir modda uchun o’zining kritik temperaturasi va bosimi mavjud. Masalan, simob uchun u 1730⁰C va 1640 atm ga, suv uchun 374⁰C va 218,4 atm ga, karbonat angidrid uchun 310C va 73 atm ga, kislorod uchun – 118⁰C va 50 atm ga, vodorod uchun – 240⁰C va 12,8 atm ga, geliy uchun – 268⁰C va 2,26 atm ga tengdir. Temperatura ko’tarilishi bilan solishtirma bug’lanish issiqligi kamaya boradi va kritik temperaturada nolga teng bo’ladi.

Ikkinchi tur fazaviy o’tishning temperaturasi ham bosimga bog’liq bo’ladi. Lekin, oldin aytilganidek, issiqlik va hajmiy effektlar nolga tengdir. Bu bog’lanish fazaviy o’tish nuqtasida issiqik sig’imining, kengayish va siqilish koeffitsiyentining o’zgarishi bilan belgilanadi.

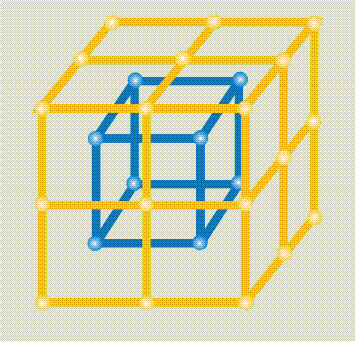
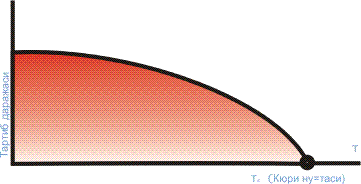
Ikkinchi tur fazaviy o’tishlar tartibning o’zgarishi bilan bog’liq. Buni beta-jez – mis va rux qotishmasidagi fazaviy o’tish misolida tushunib olish mumkin. Och rangli doirachalar bilan tasvirlangan mis atomlari kub uchlarida, rux atomlari (qora doirachalar) esa markazida (yoki aksincha) joylashgan bo’ladi. Har bir mis atomiga faqat rux atomlari ideal tartibda eng yaqin qo’shni bo’lib joylashadi. Biroq temperatura ko’tarilgan sari atomning «begona» tugunni egallash ehtimoli ortaboradi. Bu ehtimolliklar dagi (ω₁ – «o’z» tugunini egallash ehtimoli va – «begona» tugunni egallash ehtimoli) har xil (atomlar ko’proq «o’z» «tugunlari»da «o’tiradilar») bo’lib turganda tugunlar ekvivalent bo’lmaydi hamda simmetriya (hajmiy diagonalning yarmiga siljigan holda bir-birining ichiga quyilgan ikkita kub panjaralar) o’zgarmaydi. Bu past temperaturaviy tartiblangan fazadir. Biroq fazaviy o’tish temperaturasidan katta yoki unga teng biror temperaturada (T_s – Kyuri nuqtasi deyilib, u 1895 yilda T_s=770⁰S temperatura mavjudligini ochgan frantsuz fizigi P. Kyuri sharafiga quyilgan, bundan yuqori temperaturalarda temirning ferromagnitik xossalari yo’qoladi) ω₁=ω₂ bo’lib qoladi. Endi barcha tugunlar ekvivalent bo’lib, simmetriya ortadi: beta-jez hajmiy-markazlashgan kub panjaraga ega bo’lib qoladi. Yangi, yanada yuqoriroq simmetriyali yuqori temperaturaviy tartibsizlangan faza vujudga keladi. Tartib darajasini kiritish mumkin μ=(ω₁-ω₂):(ω₁+ω₂) To’liq tartiblangan holatda, absolyut nol temperaturada ω₁=1, ω₂=0, (barcha atomlar «o’z» tugunlarida «o’tiradi») va μ=1, to’liq tartibsizlangan (T ≥ Ts) holatda esa ω₁=ω₂=1/2 1/2 (barcha tugunlar birday) va μ=0. Istalgan har qanday kichik μ>0 da simmetriya yetarlicha tartiblangan fazadagidek bo’ladi. Boshqa ikkinchi tur fazaviy o’tishlar ham shunga o’xshash tarzda tushuntiriladi. Masalan, temir T dan pastda ferromagnitik xossalarga, yuqorida esa paramagnetik xossalarga egadir (Magnetizm). Qizdirganda ferromagnetizmning yo’qolishi magnit momentlar – spinlar joylashuvidagi tartibning o’zgarishi bilan bog’liqdir.

T_c yaqinida tartib darajasi nolga istalgancha yaqin bo’ladi. Shu sababli, ikkinchi tur fazaviy o’tish energiya sarfini talab qilmaydi: issiqlik va hajmiy effektlar nolga teng bo’ladi. Tartiblanmagan qotishmani tartiblangan holatgacha o’ta sovitish mumkin emasligi ham shu bilan tushuntiriladi.