1900 yilda M. Plank devorlari qizdirilgan yashik teshigidan chiqayotgan nurlanishlarning chastotalar bo’yicha taqsimlanishini tushuntirishning yagona imkoniyati borligini aniqladi (Fizik paradokslar): ω chastotali to’lqinlarni nurlayotgan zarralar o’z energiyasini faqat sakrab-sakrab, ya’ni ℏ•ω ulushlar bilan o’zgartirishlari mumkin. ℏ koeffitsiyent Plank doimiysi deb ataladi.

SHunga asoslanib, Plank o’zining mashhur formulasini topgan. Bu formula barcha chastotalar va devorlarning har qanday temperaturasi uchun nurlanish intensivligining eksperimental tarqalishini g’oyat katta aniqlik bilan ifodalagan. Klassik fizika bunday sakrashlarni bilmas edi, chunki ℏ kichikligi tufayli energiya sakrashlari shunday kichik ediki, o’zgarishlar uzluksizdek bo’lib tuyulardi.

1905 yilda sakrashsimonlik A.Eynshteyning fotoeffekt nazariyasiga oid ishi bilan tasdiqlandi. YOrug’lik - bu zarralar to’plami - fotonlar bo’lib, ular elektron bilan o’zaro ta’sirlashganda uni atomdan chiqarib tashlaydi, deb taxmin qilibgina fotoeffektni tushuntirish mumkin. YOrug’likni klassik elektromagnit to’lqin kabi tasavvur qilib, elektronni atomdan chiqarish uchun zarur energiya bir elektronda to’planishini tushuntirib bo’lmas edi. Eynshteyn ε energiyali foton 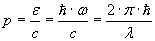impulsiga ega ekanini ko’rsatdi.Berilgan chastotali to’lqin energiyasi Plank mulohazasidagi nurlangichlar energiyasiga o’xshab, faqat sakrashsimon, ℏ•ω ulushlar bilan o’zgarishi mumkin. Sakrashsimonlik g’oyasi elektromagnit to’lqinlarga ham tarqaldi.

Ma’lum darajada Eynshteynning nuqtai nazari Nyutonning korpuskulalar nazariyasiga qaytishni bildirardi (Optika, Foton) I. Nyuton javob topa olmagan savol yana paydo bo’ldi: interferentsiya va difraktsiyaga oid tajribalarda isbotlangan yorug’likning to’lqin tabiatini fotoeffektni tushuntirish uchun zarur korpuskulyar tabiat bilan qanday bog’lash mumkin?

1913 yilda N. Bor nurlangichlar energiyalari olishi mumkin bo’lgan qiymatlarining diskretligi haqidagi g’oyani atomga tatbiq qildi: bu barcha orbitalar uchun emas, ba’zilarigagina tegishlidir. Bor ana shu tegishli orbitalarni topish qoidasini aniqladi. Klassik nuqtai nazardan yondashilganda yadro atrofida aylanayotgan elektron elektromagnit to’lqinlar tarqatishi kerak. U tezlanish bilan harakatlanadi; klassik elektrodinamika qonunlariga ko’ra esa to’g’ri chiziq bo’ylab o’zgarmas tezlikda harakatlanayotgan zaryadgina nurlanmaydi. Nima uchun yorug’lik chiqarayotgan elektron yadroga tushmaydi?

Bor qoidasiga ko’ra, elektron faqat bir orbitadan ikkinchisiga o’tayotgandagina ω chastotali ulushda yorug’lik nurlanish mumkin: ω=(E_n-E_m)/ℏ bunda E_n va E_m lar n^- va m- orbitalardagi elektron energiyasi qiymatlari. Eng kichik qiymat olishi mumkin bo’lgan energiyali orbitada elektron cheksiz uzoq yashashi mumkin - u hech qaerga o’ta olmaydi. Atomlarning turg’unligi ana shunday tushuntirilgan edi.

Bor nazariyasi atomlarning barcha asosiy xossalarini tushuntirib berdi, lekin kvantlash qoidalarining ma’nosi jumboqligicha qoldi. Bor ularni postulatlar - isbotlanmagan taxminlar deb atadi. Kvant mexanika yaratilgandan keyingina ularning ma’nosi tushunarli bo’ldi.

Borning kvantlash qoidasi - fan tarixidagi g’aroyib hodisalardan biridir. Zarralarning to’lqin xossalari aniqlangunga qadar bu nazariyaning paydo bo’lishini buyuk zakovat samarasi bilangina tushuntirish mumkin. Bu borada Eynshteyn: «Bu nazariy fikr sohasidagi oliy musiqaviylikdir» degan edi.

1924 yilda frantsuz olimi L. de Broyl taxminiga ko’ra, zarralar, masalan, elektronlarning harakati, xuddi fotonlarning to’lqin uzunligi ularning impulsi bilan bog’liq bo’lganidek, λ to’lqin uzunligi, p harakat miqdori bilan bog’liq bo’lgan to’lqin protsessi orqali bayon qilinishi lozim: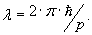

Uch yil o’tmasdanoq bu taxmin tajribada tasdiqlandi: amerika fiziklarn K. Devisson va L. Jermer kristallarda elektronlar difraktsiyasini kashf qilishdi - haqiqatan ham, elektron o’zini to’lqin kabi tutadi. Kristalldan o’tgandan so’ng difraktsion dog’larning joylashishiga ko’ra ayni energiyali elektron bilan bog’liq bo’lgan to’lqin uzunligini topish mumkin bo’ldi. Bu esa de Broyl bashoratiga mos keldi.

Navbatdagi muhim voqea 1926 yilda yuz berdi. Avstriya olimi E. SHryodinger elektron erkin fazoda emas, balki tashqi maydonda, masalan, yadroning Kulon maydonida harakatlanadi, degan hol uchun de Broyl jumbog’ini umumlashtirdi. U zarralarning to’lqin xossalarini ifodalaydigan funktsiya uchun tenglama yaratdi. Erkin fazoda bu tenglama yechimi de Broyl to’lqin uzunligidagi to’lqin protsessini ifodalaydigan funktsiyaga o’tadi. Tashqi maydonda to’lqin uzunligi nuqtadan nuqtagacha o’zgaradi. Vodorod atomida elektronning statsionar holati SHryodinger tenglamasida turg’un to’lqin hosil bo’lganini bildiradi. Buning uchun elektronning harakat sohasiga de Broyl to’lqinlarining yaxlit soni joylashishi lozim. Bor kvantlash qoidasining ma’nosi ham ana shundan iborat. Elektron energiyasining faqat diskret qiymatlarida, ya’ni 1,2 va h.k. to’lqinlar joylashadigan hollardagina turg’un to’lqinlar paydo bo’ladi. Energiyaning diskret sathlari qanday paydo bo’lishiga oddiy misol keltiramiz. Faraz qilaylik, zarra l uzunlikdagi interval ichida yoki boshqachasiga aytganda, cheksiz devorli l uzunlikdagi potentsial o’ra ichida bir yo’nalishda harakat qilmoqda. O’ra chetlarida to’lqin funktsiyasi nolga aylanishi kerak. Statsionar holat ushbu shartdan hosil bo’ladi: l uzunlikda yarim to’lqinlarning yaxlit soni joylashishi lozim: 2•l/λ=n Endi de Broyl to’lqin uzunligini zarra impulsi bilan bog’laydigan formuladan foydalanamiz: p=2•π•ℏ/λ=&pi•ℏ•n/l, E=p²/2•m energiyani topamiz. Ushbu formulani olish qiyin emas: E=π²•ℏ²•n²/2•m•l² Ancha murakkabroq hollar uchun energiya sathlarini ham shu usulda topish mumkin.

SHryodinger tenglamasi potentsial V^(x) da bir o’lchovli harakat uchun ushbu ko’rinishni oladi: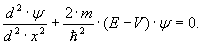

Birinchi qo’shiluvchi - x bo’yicha ikkinchi hosila ψ . Agar birinchi hosila ψ ning x dan o’zgarish tezligini ifodalasa, ikkinchi hosila shu tezlikning o’zgarish tezligini beradi.

Bu tenglamaning V=0 uchun yechimini topish oson. Bu yechimlar ikkita: ψ₁=α₁•sinkx va ψ₂=α₂•coskx Ana shular de Broyl to’lqinlarini ifodalaydi: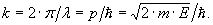

Muvozanat holati atrofida tebranayotgan zarra uchun (qaytaruvchi kuch og’ish kattaligi x ga proportsional bo’lganda) potentsial V^(x) ushbu ko’rinishni oladi: V^(x)=γ•x²/2

Bunday potentsial uchun Shryodinger tenglamasini aniq yechish oson emas; faqat natijani keltiramiz. Bunday ostsillyator uchun energiyaning mumkin bo’lgan qiymatlari 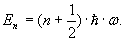. Eng past holatda (n=0) klassik ostsillyatordan farqli ravishda, kinetik energiya ham, potentsial energiya ham nolga teng bo’lmaydi. Ularning yig’indisi ℏ•ω/2 ga tenglashadi. Zarra muvozanat holat atrofida tebranadi, shuning uchun kinetik energiyaning o’rtacha qiymati potentsial energiyaning o’rtacha qiymatiga tenglashadi va ℏ•ω/4 ni tashkil qiladi.

Agar tarqalganidan so’ng elektronlar dastasining intensivligi to’lqin funktsiyasi modulining kvadratiga proportsional deb faraz qilinsa, elektronlar difraktsiyasiga oid tajribalarni ham Shryodinger tenglamasi bilan tavsiflash mumkin. Kristall panjara atomlari tarqatgan to’lqinlar qo’shiladigan joyda elektronlar dastasi maksimal intensivlikka erishadi.

Dasta intensivligi kamayganda (agar, aytaylik, minutiga bitta elektron uchib o’tganda ham) difraktsion manzara o’zgarmasligi ma’lum bo’ldi. Demak, bir elektronning o’ziyoq kristall orqasida turgan fotoplastinkaning u yoki bu joyiga tushish ehtimoli bor, deb qarash kerak.

1926 yilda nemis fizigi M. Born elektronni u yoki bu joyda topish ehtimoli to’lqin funktsiyasi moduli kvadratiga teng deb taxmin qildi. Bunday xulosaga kelishga nima yordam berdi?

YOrug’likning to’lqin hodisalari nazariyasi - interferentsiya va difraktsiya - Maksvell tenglamasidan, ya’ni yorug’likning elektromagnit tabiatini tushunishdan ancha oldin ishlab chiqilganligini eslaylik. Faqat yorug’lik manbai noma’lum tabiatli to’lqinlarni chiqarishi, yorug’lik intensivligi esa o’zgarib turadigan kattalik kvadratiga proportsional ekanligi taxmin qilinardi. Hozirgi zamon tasavvuriga ko’ra, elektr va magnit maydonlari vaqt davomida va fazoda o’zgaradi, yorug’lik intensivligi ularning kvadratiga proportsionaldir. Lekin deyarli barcha to’lqin hodisalari yorug’lik tabiatidan mustaqil tarzda tushuntiriladi.

Zarralar bilan bog’liq bo’lgan to’lqinlar uchun ham to’lqin protsess mavjud, intensivlik (bizning holda ehtimollik) to’lqin funktsiyasi moduli kvadratiga proportsional ekan, deb hisoblash tabiiy edi.

Dastlab, yorug’lik to’lqinidagi elektromagnit maydonga o’xshash zarraning to’lqin xossalariga muayyan real fizik maydon mos keladi, deb taxmin qilishgan edi. Lekin u holda bir elektronning o’zi bir aktda butun difraktsion manzarani hosil qilgan bo’lardi, holbuki u fotoplastinkaning faqat bir donini qoraytiradi. Bu dalil to’lqin protsess tabiatiga bunday qarashga qarshi yagona dalil emas.

SHunday qilib, zarraning to’lqin funktsiyasi biror bir fizik maydon emas: u navbatdagi u yoki bu kuzatish natijasining potentsial imkoniyatlarini ifodalaydi.

V. Geyzenberg noaniqliklar munosabatini (1927) topgandan so’ng va ayniqsa, N. Borning A. Eynshteyn bilan ko’p yillik munozaralarida to’lqin funktsiyasining asl ma’nosi ochildi.

Kvant mexanika ba’zi masalalarning aniq javobini bermaydi, balki u yoki bu natijaning ehtimolligini tushuntiradi. Kvant mexanikaning asosiy kashfiyoti - bashoratlarning ehtimoliy xarakteri - biz aniq ma’noga ega bo’lmagan klassik tushunchalardan foydalanishimiz oqibatidir (Noaniqliklar munosabati).

Ingliz fizigi P. Dirak ishlarida kvant mexanika yanada rivojlantirildi. U Shryodinger tenglamasini yorug’lik tezligiga tenglashadigan tezlikda harakatlanadigan 1/2 spinli zarralar uchun umumlashtirdi. Dirak tenglamasining asosiy xulosasi shuki, zarralar bilan birga ulardan faqat zaryadining ishorasi bilan farqlanadigan antizarralar (masalan, elektron bilan birga - pozitron) ham mavjud bo’lishi lozim.

1930 yilda E. Fermi kvant mexanikani elektromagnit maydonga tatbiq qildi. To’lqin vektori k bo’lgan to’lqin elektr va magnit maydonlari tebranadigan ostsillyatordir. Magnit maydon energiyasi ostsillyatorning potentsial energiyasi, elektr maydon energiyasi esa kinetik energiya rolini o’taydi. Biroq kvant mexanikani ostsillyatorga tatbiq qilish shunga olib keladiki, ostsillyator energiyasi ℏ•ω qiymatli ulushlar bilan o’zgarishi mumkin; bundan tashqari, eng past energiyali holatda kinetik va potentsial energiyalar nolga teng bo’lmaydi. Birorta zarra, birorta kvant bo’lmagan vakuumda har qaysi to’lqin vektori uchun elektr va magnit maydonlari qiymati nol yaqinida turadi. Bo’shlikda elektromagnit maydonning nolinchi tebranishlari mavjud bo’ladi. Agar biror to’lqin vektori uchun energiya eng past qiymatdan biriichi uyg’ongan holatga o’tsa, fazoda to’lqin vektori k, energiyasi ε=ℏ•k•c, impulsi p=ℏ•k bo’lgan bitta kvant paydo bo’ladi, deyiladi. Ana shu 1905 yilda Eynshteyn bashorat qilgan fotondir.

SHryodinger tenglamasiga ko’ra, atom istalgan uyg’ongan holatda cheksiz uzoq muddat bo’lishi lozim. Ayni nolinchi tebranishlar elektronni ancha past orbitaga o’tib, yorug’lik kvantni - foton chiqarishga majbur qiladi.

Kvant mexanikani boshqa maydonlarga, masalan, bayon qilinayotgan elektron va pozitronlarga qo’llash xuddi shunday natijaga olib keladi - vakuumda elektron - pozitron maydonning nolinchi tebranishlari mavjud, har xil zarralar uzluksiz paydo bo’lib va yo’qolib turadi. Bunday vaqtincha paydo bo’ladigan zarralar virtual zarralar deb ataladi (Fizik vakuum).