Engil sterjen bilan bir-biriga r masofada biriktirilgan t₁ va t₂ massali ikki yukin tasavvur qilaylik. Bunday yuklar endi o’zlarini mustaqil tuta olmaydi, ular bitta sistemani tashkil qiladi. Agar t₁ yukka tashqi kuch qo’yilsa, u holda t₂ yuk ham tezlashadi va aksincha. Bunday sistemaning harakatini yaxshiroq qanday tavsiflash mumkin?

Ma’lum bo’lishicha, bitta maxsus nuqta mavjud bo’lib, u nuqta unga butun sistema massasi joylanganda va barcha tashqi kuchlar (ichki kuchlarni hisobga olmasa ham bo’ladi, chunki ularning vektor yig’indisi Nyutonning uchinchi qonuniga ko’ra nolga teng) qo’yilganda qanday harakat qilsa, shunday harakat qilar ekan. Masalan, yuklar og’irlik maydoniga tashlansa, ular yumalaydi, lekin sistemaning bitta nuqtasi odatdagidek parabola bo’yicha harakat qiladi. Bu nuqta massalar markazi deyiladi. U istagan, hatto, eng murakkab sistemada ham bo’ladi.

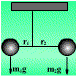
Massalar markazining holatini qanday qilib topish mumkin? Agar yukli sterjen osib qo’yilsa, u holda osmaning tanlangan ma’lum nuqtasida sterjen gorizontal holatda muvozanatda qoladi. Buning uchun m₁r₁= m₂r₂ shart bajarilishi, ya’ni og’irlik kuchlari momentlari osma nuqtasiga nisbatan teng bo’lishi kerak. Ikkinchi tomondan, ta’rifga ko’ra butun sistema massasi massalar markazida to’plangani uchun og’irlik kuchining teng ta’sir etuvchisi nam massalar markazidan o’tishi shart (shuning uchun u sistemaning og’irlik markazi deb ham ataladi).

Yukli sterjenning massalar markazini aniqlash.

Elektron-pozitron juftining hosil bo’lishi va massalar markazi sistemasida annigilyatsiyasi.

Binobarin muvozanatda, aylanish bo’lmaganda massalar markazi osma nuqtasi bilan mos tushishi kerak. Albatta, massalar markazining holatini eksperimental topish shart emas. Uni yuqorida ifodalangan formuladan foydalanib hisoblash mumkin: massalar markazi yuklarni biriktiruvchi chiziqda t₁ yukdan r₁=rm₂/(m₁+m₂) masofada yoki yukdan r₂=rm₁/(m₁+m₂) masofada joylashgan bo’ladi. Agar yuklar ko’p bo’lsa, u holda sistemani ketma-ket juftlarga bo’lib, butun sistemaning massalar markazi holatini topish mumkin.

Demak, massalar markazi sistemaning tashqi kuchlar ta’siridagi, ichki harakatga ahamiyat bermagan holda, keng ko’lamli harakatini tavsiflashga imkon beradi. Xususan, agar jismga tashqi kuchlar ta’sir etmasa (yoki ularning vektor yig’indisi nolga teng bo’lsa), u holda massalar markazi doimiy tezlik bilan harakatlanishi kerak. Agar u dastlab tinch turgan bo’lsa, uning siljishi nolga teng bo’ladi. Izolyatsiyalangan sistemaning massalar markazi joyida qoladi. Mana shuning uchun juda sirg’anchiq muzda yugurish, yoqilg’ini orqaga chiqarmay turib raketani o’chirish va h.k. qilish mumkin emas. Bu xossa tabiatning juda muhim qonunini - impulsning saqlanish qonunini aks ettiradi.

Ikkinchi tomondan, bizni sistemadagn ichki jarayonlar qiziqtirsa, bu sistemaning harakatini bir butun deb qarashdan chetlashish uchun massalar markazi (massalar markazi sistemasi) bilan bog’lik bo’lgan sanoq sistemasiga o’tish mumkin.

Izolyatsiyalangan sistema uchun massalar markazi doimiy tezlik bilan harakatlanadi va bunday sistema inersial sistema bo’ladi.

Ma’lumki, masalan, γ-kvantlar zarralar jufti: elektron va pozitronni hosil qiladi. Lekin bu jarayon bitta kvant bilan sodir bo’lmas ekan. Bunga ishonish uchun massalar markazi sistemasidan foydalanamiz. Bu sistemada elektron va pozitronning yig’indi impulsi nolga teng (zarralarning massalari bir xil bo’lgani uchun massalar markazi hamisha o’ratada bo’ladi va zarralar unga nisbatan har xil tomonga bir xil kattalikdagi tezlik bilan uchib ketadi). Ayni vaqtda zarralar hosil bo’lgan γ-kvanti impulsi noldan farqli bo’ladi, chunki istagan sanoq sistemasida u yorug’lik tezligiga teng tezlik bilan harakatlanadi. Shuning uchun nmpulsning saqlanish qonuni bunday jarayonni man qiladi. Bu jarayon, masalan, ikkita γ-kvantning to’qnashishida yoki qo’shimcha impuls beriladigan boshqa zarralar ham bo’lganda sodir bo’ladi. Xuddi shunga o’xshash annigilyatsiyada ikkita γ-kvant hosil bo’ladi. Ko’rinib turibdiki, massalar markazi sistemasida zarralarning o’zaro ta’siri jarayonini tekshirish qulay va bunday sistemadan yadro fizikasi va elementar zarralar fizikasida keng foydalaniladi.